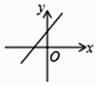
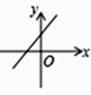
 B.
B. 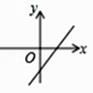 C.
C. 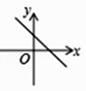 D.
D. 







把图①看作一个大正方形,它的面积是( 如果把图①看作是由2 个长方形和2个小正方形组成的,它的面积为
由此得到:


素材1:如图1,圆柱体的高AC为12cm,底面直径BC为6cm,在圆柱下底圆周上的A点有一只蚂蚁,它想吃到上底面圆周上与A 点对应的B 点处的食物.
若蚂蚁沿图1中的折线A→C→B爬行的最短路径记为“路线一”,此时最短路程是 12+6=18cm. 将圆柱沿着AC将侧面展开得到图2,请在图2中画出蚂蚁爬行的最短路径记为“路线二”,此时最短路程是____ cm; 比较可知:蚂蚁爬行的最短路径是路线____(用“一”或“二”填空).


素材2:如图3所示的实践活动器材包括:底面直径为6cm,高为10cm的圆柱、橡皮筋、细线(借助细线来反映爬行的路线)、直尺,通过调节橡皮筋的位置达到改变圆柱的高度的目的.